Q:
Two parallel chords on the same side of the centre of a circle are 5 cm apart. If the chords are 20 and 28 cm long, what is the radius of the circle?
Answer & Explanation
Answer: B) 15.69 cm
Explanation: 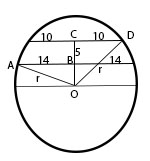
Draw the two chords as shown in the figure. Let O be the center of the circle. Draw OC
perpendicular to both chords. That divides the two chords in half.
So CD = 10 and AB = 14. Draw radii OA and OD, both equal to radius r.
We are given that BC = 5, the distance between the two chords. Let
OB = x.
We use the Pythagorean theorem on right triangle ABO
AO² = AB² + OB²
r² = 14² + x²
We use the Pythagorean theorem on right triangle DCO
DO² = CD² + OC²
We see that OC = OB+BC = x+5, so
r² = 10² + (x+5)²
So we have a system of two equations:
r² = 14² + x²
r² = 10² + (x+5)²
Since both left sides equal r², set the right sides
equal to each other.
14² + x² = 10² + (x+5)²
196 + x² = 100 + x² + 10x + 25
196 = 125 + 10x
71 = 10x
7.1 = x
r² = 14² + x²
r² = 196 + (7.1)²
r² = 196 + 50.41
r² = 246.41
r = √246.41
r = 15.69745202 cm
View Answer
Report Error
Discuss